Multi Degree of Freedom Holonomic System#
In this example we demonstrate the use of the functionality provided in
sympy.physics.mechanics for deriving the equations of motion (EOM) of a holonomic
system that includes both particles and rigid bodies with contributing forces and torques,
some of which are specified forces and torques. The system is shown below:
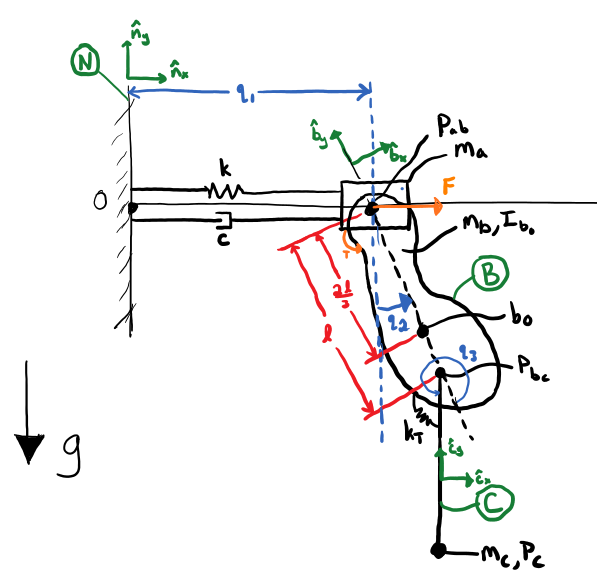
The system will be modeled using JointsMethod. First we need to create the
dynamicsymbols needed to describe the system as shown in the above diagram.
In this case, the generalized coordinates \(q_1\) represent lateral distance of block from wall,
\(q_2\) represents ngle of the compound pendulum from vertical, \(q_3\) represents angle of the simple
pendulum from the compound pendulum. The generalized speeds \(u_1\) represents lateral speed of block,
\(u_2\) represents lateral speed of compound pendulum and \(u_3\) represents angular speed of C relative to B.
We also create some symbols to represent the length and
mass of the pendulum, as well as gravity and others.
>>> from sympy import zeros, symbols
>>> from sympy.physics.mechanics import Body, PinJoint, PrismaticJoint, JointsMethod, inertia
>>> from sympy.physics.mechanics import dynamicsymbols
>>> q1, q2, q3, u1, u2, u3 = dynamicsymbols('q1, q2, q3, u1, u2, u3')
>>> l, k, c, g, kT = symbols('l, k, c, g, kT')
>>> ma, mb, mc, IBzz= symbols('ma, mb, mc, IBzz')
Next, we create the bodies and connect them using joints to establish the kinematics.
>>> wall = Body('N')
>>> block = Body('A', mass=ma)
>>> IB = inertia(block.frame, 0, 0, IBzz)
>>> compound_pend = Body('B', mass=mb, central_inertia=IB)
>>> simple_pend = Body('C', mass=mc)
>>> bodies = (wall, block, compound_pend, simple_pend)
>>> slider = PrismaticJoint('J1', wall, block, coordinates=q1, speeds=u1)
>>> rev1 = PinJoint('J2', block, compound_pend, coordinates=q2, speeds=u2,
... child_axis=compound_pend.z, child_joint_pos=l*2/3*compound_pend.y,
... parent_axis=block.z)
>>> rev2 = PinJoint('J3', compound_pend, simple_pend, coordinates=q3, speeds=u3,
... child_axis=simple_pend.z, parent_joint_pos=-l/3*compound_pend.y,
... parent_axis=compound_pend.z, child_joint_pos=l*simple_pend.y)
>>> joints = (slider, rev1, rev2)
Now we can apply loads (forces and torques) to the bodies, gravity acts on all bodies, a linear spring and damper act on block and wall, a rotational linear spring acts on C relative to B specified torque T acts on compound_pend and block, specified force F acts on block.
>>> F, T = dynamicsymbols('F, T')
>>> block.apply_force(F*block.x)
>>> block.apply_force(-k*q1*block.x, reaction_body=wall)
>>> block.apply_force(-c*u1*block.x, reaction_body=wall)
>>> compound_pend.apply_torque(T*compound_pend.z, reaction_body=block)
>>> simple_pend.apply_torque(kT*q3*simple_pend.z, reaction_body=compound_pend)
>>> block.apply_force(-wall.y*block.mass*g)
>>> compound_pend.apply_force(-wall.y*compound_pend.mass*g)
>>> simple_pend.apply_force(-wall.y*simple_pend.mass*g)
With the problem setup, the equations of motion can be generated using the
JointsMethod class with KanesMethod in backend.
>>> method = JointsMethod(wall, slider, rev1, rev2)
>>> method.form_eoms()
Matrix([
[ -c*u1(t) - k*q1(t) + 2*l*mb*u2(t)**2*sin(q2(t))/3 - l*mc*(-sin(q2(t))*cos(q3(t)) - sin(q3(t))*cos(q2(t)))*(u2(t) + u3(t))*u3(t) - mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))/3)*Derivative(u3(t), t) + mc*(2*l*u2(t)/3 + l*u3(t)/3)*u2(t)*sin(q2(t)) - (2*l*mb*cos(q2(t))/3 + 2*l*mc*cos(q2(t))/3)*Derivative(u2(t), t) - (ma + mb + mc)*Derivative(u1(t), t) + F(t)],
[ -2*g*l*mb*sin(q2(t))/3 - 2*g*l*mc*sin(q2(t))/3 + 2*l**2*mc*(u2(t) + u3(t))*u3(t)*sin(q3(t))/3 - mc*(2*l**2*cos(q3(t))/3 + 2*l**2/9)*Derivative(u3(t), t) - (2*l*mb*cos(q2(t))/3 + 2*l*mc*cos(q2(t))/3)*Derivative(u1(t), t) - (IBzz + 4*l**2*mb/9 + 4*l**2*mc/9)*Derivative(u2(t), t) + T(t)],
[-g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - g*l*mc*sin(q2(t))/3 + kT*q3(t) + l**2*mc*(u2(t) + u3(t))*u3(t)*sin(q3(t))/3 - l*mc*(2*l*u2(t)/3 + l*u3(t)/3)*u2(t)*sin(q3(t)) - mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))/3)*Derivative(u1(t), t) - mc*(2*l**2*cos(q3(t))/3 + 2*l**2/9)*Derivative(u2(t), t) - mc*(2*l**2*cos(q3(t))/3 + 10*l**2/9)*Derivative(u3(t), t)]])
>>> method.mass_matrix_full
Matrix([
[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, ma + mb + mc, 2*l*mb*cos(q2(t))/3 + 2*l*mc*cos(q2(t))/3, mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))/3)],
[0, 0, 0, 2*l*mb*cos(q2(t))/3 + 2*l*mc*cos(q2(t))/3, IBzz + 4*l**2*mb/9 + 4*l**2*mc/9, mc*(2*l**2*cos(q3(t))/3 + 2*l**2/9)],
[0, 0, 0, mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))/3), mc*(2*l**2*cos(q3(t))/3 + 2*l**2/9), mc*(2*l**2*cos(q3(t))/3 + 10*l**2/9)]])
>>> method.forcing_full
Matrix([
[ u1(t)],
[ u2(t)],
[ u3(t)],
[ -c*u1(t) - k*q1(t) + 2*l*mb*u2(t)**2*sin(q2(t))/3 - l*mc*(-sin(q2(t))*cos(q3(t)) - sin(q3(t))*cos(q2(t)))*(u2(t) + u3(t))*u3(t) + mc*(2*l*u2(t)/3 + l*u3(t)/3)*u2(t)*sin(q2(t)) + F(t)],
[ -2*g*l*mb*sin(q2(t))/3 - 2*g*l*mc*sin(q2(t))/3 + 2*l**2*mc*(u2(t) + u3(t))*u3(t)*sin(q3(t))/3 + T(t)],
[-g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - g*l*mc*sin(q2(t))/3 + kT*q3(t) + l**2*mc*(u2(t) + u3(t))*u3(t)*sin(q3(t))/3 - l*mc*(2*l*u2(t)/3 + l*u3(t)/3)*u2(t)*sin(q3(t))]])